Python에서의 반올림과 소수 계산

이 글은 Python 3.7 기준으로 작성되었습니다.

우리가 흔히 알고 있는 반올림

우리가 흔히 알고 있는 반올림은 반올림 대상의 자릿수가 4이하일 때는 0으로 버리고 5이상이면 일 때는 올림하는 사사오입(四捨五入) 방식을 사용한다.

이 방식으로 소수점 아래 첫째 자리에서 반올림 했을 때의 결과는 아래와 같은데, 어쩌면 너무나도 당연한 결과이며 C, C++, Java에서도 동일한 결과가 나타난다.

수	반올림 결과
0.4	0
0.5	1
1.5	2
2.5	3
2.6	3
3.5	4

Python에서는 어떨까?

하지만 이러한 반올림 연산을 Python에서 사용하면 어떨까?

Python에서 제공하는 기본 round 함수를 이용한 결과는 다음과 같다.

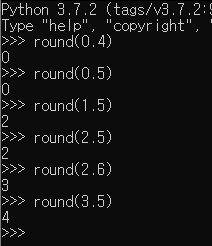
수	우리가 생각했던 반올림 결과	Python 3.x
0.4	0	0
0.5	1	0
1.5	2	2
2.5	3	2
2.6	3	3
3.5	4	4

0.5 를 반올림했는데 어째서 0이며, 2.5를 반올림했는데 어째서 2 인가?

이러한 결과가 나오는 이유는 Python 3.x부터 rounding 방식이 변경되었고 그 방식은 우리가 알고 있는 반올림 방식과 다르게 작동하기 때문이다.

Python 2.x에서는 우리가 흔히 알고 있는 사사오입 방식(Round half away from zero)을 이용한다.

하지만 Python 3.x에서는 Round half to even 이라는 반올림 방식이 적용되었는데 이것은 가장 가까운 2의 배수로 근사시키는 방식이다. Banker’s Rounding이라고도 부른다.

Banker’s Rounding

Banker’s Rounding은 아래의 규칙에 의해 반올림을 수행한다.

• 반올림 대상의 자리가 5 미만일 때는 버리고 5 초과일 때는 올린다.

• 반올림 대상의 자리가 5 인 경우에는 두 가지의 경우로 구분한다.

  • 반올림 대상의 앞자리가 2의 배수인 경우에는 버린다. (2.5 -> 2)

  • 반올림 대상의 앞자리가 2의 배수가 아닌 경우에는 올린다. (1.5->2, 3.5 -> 4)

이 방법은 일반적으로 생각하는 반올림 상식에 어긋나지만 정확한 반올림을 위해 고안되었다고 하며 다음과 같은 정당성을 갖게 된다.

4.0 부터 5.0 사이를 0.1씩의 간격으로 나누면 9개의 값으로 나누어 진다.
(4.1, 4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8, 4.9) 그리고 이 값들은 반올림의 대상이다.
상식적인 반올림의 경우 9개의 값 중에서 4개는 버림을 수행하고 5개는 올림을 수행한다.
올림을 수행하는 수의 개수가 1개 더 많다.

그러나 0.5에서 가장 가까운 2의 배수로 근사시키면 이 문제를 해결할 수 있다.
4.0 부터 6.0 사이를 0.1씩의 간격으로 나누면 18개의 값으로 나누어지고,
버리는 쪽과 올리는 쪽이 9개씩 나누어 갖게 되면서 어느 한쪽에 치우치지 않는 공평한 셈이 된다.
4.1, 4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8, 4.9
5.1, 5.2, 5.3, 5.4, 5.5, 5.6, 5.7, 5.8, 5.9

이처럼 우리가 흔히 알고있는 반올림 방식이 ‘올림을 수행하는 수의 개수가 1개 더 많다.’는 이유로 인하여, 해외의 어느 나라에서는 세금을 계산할 때 부당하게 세금을 더 챙겨간다는 문제가 제기되었다고 하는데, 실제 일인지는 찾지 못하였기 때문에 이 사례의 진위여부 보다는 ‘반올림 문제로 인하여 예상하지 못한 일이 일어날수 있으니 주의해야 한다’ 라는 인식을 갖자.

(가령 4.25 학점을 소수점 아래 둘째 자리에서 반올림할 때 Banker’s Rounding 방식을 적용하면 4.3이 아니라 4.2가 된다.)

실수형에 대해 round 함수 사용

이제 Python 3.x 반올림이 Round half to even 방식을 채택하고 있다는 것을 알게 되었다.

Banker’s Rounding 방식의 다른 예시를 round 함수를 통해 살펴보자.

참고 : Python에서 round() 함수의 작동

round(number, [ndigits])
# number : 반올림하려는 값
# ndigits : 반올림을 수행할 자릿 수 (default : 소수점 아래 첫째자리)

round(number, -2) # 십의 자리에서 반올림
round(number, -1) # 일의 자리에서 반올림
round(number, 0)  # 소수점 아래 첫째 자리에서 반올림
round(number, 1)  # 소수점 아래 둘째 자리에서 반올림
round(number, 2)  # 소수점 아래 셋째 자리에서 반올림

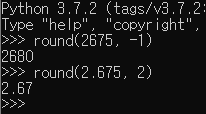
2675 값에 대해 1의 자리에서 반올림하면 2680이다. (valid)

2.675 값에 대해 소수점 아래 셋째 자리에서 반올림하면 2.67이다. (invalid)

2.675 를 소수점 아래 셋째 자리에서 반올림 할 때 2.68 이 되어야 하는데 ?

2.675 를 소수점 아래 셋째 자리에서 반올림하면 2.68 이 되어야 하는데 2.67 이라는 결과가 나온다.

이러한 값이 나온 이유는 대부분의 primitive type(float, double 등)으로 소수를 정확히 표현할 수 없기 때문이다.

소수점 연산 오차의 사례

소수점 연산 오차는 반올림에서만 존재하는 것이 아니다.

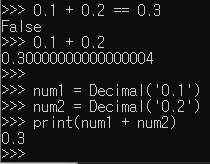
수식 0.1 + 0.2 == 0.3의 결과는 True가 나올것으로 예상되지만 그렇지 않다.

0.1과 0.2가 실제로는 근삿값으로 저장되어 있기 때문이다.

(decimal은 정확한 계산을 도와주는 라이브러리이며 어떤 실수의 실제 표현이 어떻게 되어있는지 확인할 수 있다.)

정확한 계산을 도와주는 decimal

컴퓨터는 사람들이 학교에서 배우는 산술과 동일한 방식으로 작동하는 산술을 제공해야 합니다. - decimal arithmetic specification

지금까지 살펴봤던 실수 오차 문제를 해결하기 위해 좀 더 정확한 계산을 도와주는 라이브러리가 제공된다.

그렇다면 모든 실수가 근삿값으로 저장될까?

물론 모든 실수가 근삿값으로 저장되는 것은 아니며, 2의 승수로 표현될 수 있는 실수는 오차없이 그대로 저장된다.

1        = 2^0
0.5      = 2^(-1)
0.25     = 2^(-2)
0.125    = 2^(-3)
0.0625   = 2^(-4)
0.03125  = 2^(-5)
0.015625 = 2^(-6)
...

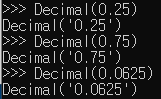
2의 승수로 표현될 수 없는 소수를 근사값으로 저장하게 되는데, 다시 이전 예제 round(2.675, 2)를 확인해보자.

Decimal 모듈을 이용해보면 2.675 의 실제 표현은 2.67499999999999982236431605997495353221893310546875가 된다.

따라서 2.675 의 실제표현 2.67499999999999982236431605997495353221893310546875를 반올림한 결과로 2.67이 된 것이다.

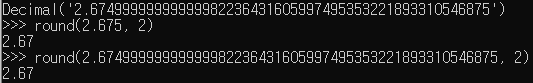
decimal 라이브러리를 이용하여 이 문제를 해결할 수 있는데, Decimal('2.675')는 우리가 생각하는 실제 2.675를 의미하고, 따라서 아래의 연산 결과는 우리가 예상하는 결과(2.68)와 동일하다.

(Decimal 매개변수에 일반적인 숫자가 아닌, 따옴표를 붙인 문자열 형태로 전달하면 그 수는 정확하게 표현된다.)

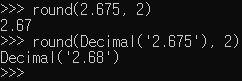
이처럼 정확한 계산을 할 때는 decimal을 이용할 수 있다.

그리고 rounding 방식을 변경할 수 있는 함수를 제공하고 있다.

마침

매우 오래전부터 사용된 소프트웨어는 일관성과 라운딩 방식을 변경한 후 달라질 정합성으로 인해 기본 함수의 방식을 무조건 변경하지는 않고, 별도로 Banker’s Rounding 방식을 사용한 함수를 사용할 수 있게 제공하고 있다.

하지만 Banker’s Rounding 방식이 더 권고되는 표준이기 때문에 새로 만들어지는 언어나 소프트웨어는 Banker’s Rounding을 지원해야 된다고 하는 의견도 있고, 실제로 적용되고 있다.

프로그래밍 언어나 소프트웨어에서 채택하고 있는 반올림 방식이 다르기 때문에 한 번쯤 확인해보면 좋을 것 같다.

만약 반올림이 사사오입으로 작동될 것으로 생각하고 프로그램을 작성했다면, 경우에 따라서는 의도치 않은 결과를 발생시키거나 오차의 원인을 찾기 위해 시간을 소비하게 될 수 있음에 유의하자.

참고 자료

• Link : 언어별 부동 소수점 처리 결과

• Link : 그 밖의 여러가지 반올림 방식들

• decimal 공식 문서 : decimal(한글), decimal(영문)